Chapter 5 Vector Calculus

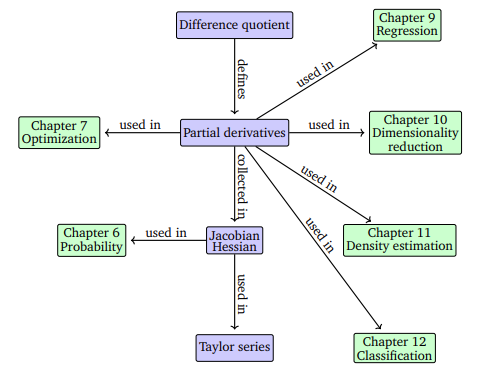
Vector calculus plays a central role in machine learning, as many algorithms involve optimizing an objective function with respect to model parameters that determine how well the model explains the data. These optimization problems often rely on gradient-based methods to find the best parameters.

Examples include:

Linear regression — optimizing linear weights to maximize likelihood (Chapter 9).
Neural network autoencoders — minimizing reconstruction error using the chain rule for derivatives.
Gaussian mixture models — optimizing location and shape parameters to best fit data distributions (Chapter 11).

A mind map of the concepts introduced in this chapter, along with when they are used in other parts of the book.

The core concept in this chapter is that of a function, which maps inputs \(\mathbf{x} \in \mathbb{R}^D\) to real-valued outputs \(f(\mathbf{x}) \in \mathbb{R}\). A function assigns each input exactly one output: \[ f : \mathbb{R}^D \to \mathbb{R}, \quad \mathbf{x} \mapsto f(\mathbf{x}) \]

Gradients are essential because they point in the direction of steepest ascent, which allows optimization algorithms to improve model performance efficiently. Thus, vector calculus provides a fundamental mathematical foundation for many learning and optimization techniques used in machine learning.

Most functions in this context are assumed to be differentiable, though extensions to sub-differentials can handle non-differentiable cases. Optimization under constraints is discussed further in Chapter 7.