4.5 Directed Graphical Models
Directed graphical models, also known as Bayesian networks, provide a graphical language for specifying probabilistic models. They offer a compact and intuitive way to visualize dependencies between random variables and to represent how a joint distribution can be decomposed into simpler conditional distributions.
The key idea is that nodes represent random variables, and edges (arrows) represent probabilistic or conditional relationships. The joint distribution is expressed as a product of conditional probabilities. Graphical models help identify independence and conditional independence relationships among variables.
Some of the benefits of graphical models are that they:
- Provide a simple way to visualize model structure.
- Facilitate the design and understanding of statistical models.
- Make independence properties easy to identify.
- Enable simplified inference and learning computations through graphical manipulations.
4.5.1 Graph Semantics
A directed graphical model (or Bayesian network) represents conditional dependencies among random variables.
Example 4.7 A joint distribution: \[ p(a, b, c) = p(c | a, b) \, p(b | a) \, p(a) \] implies the following:
- \(c\) depends on \(a\) and \(b\)
- \(b\) depends on \(a\)
- \(a\) is independent of \(b\) and \(c\)
This factorization can be represented as a directed graph with arrows from \(a \to b\) and \(a, b \to c\).
4.5.1.1 General Rule for Constructing Graphs
- Create a node for each random variable.
- For each conditional probability, draw arrows from the conditioning variables to the conditioned variable.
4.5.1.2 General Form of the Joint Distribution
For random variables \(\mathbf{x}_1, \ldots, \mathbf{x}_K\), the joint distribution factorizes as: \[ p(\mathbf{x}) = p(\mathbf{x}_1, \ldots, \mathbf{x}_K) = \prod_{k=1}^K p(\mathbf{x}_k | \text{Pa}_k) \] where \(\text{Pa}_k\) denotes the parent nodes of \(\mathbf{x}_k\) (nodes with arrows pointing to \(\mathbf{x}_k\)).
Example 4.8 Coin Flip Experiment
For a Bernoulli trial with parameter \(\mu\): \[ p(\mathbf{x} | \mu) = \text{Ber}(\mu). \] Repeating the experiment \(N\) times: \[ p(\mathbf{x}_1, \ldots, \mathbf{x}_N | \mu) = \prod_{n=1}^N p(\mathbf{x}_n | \mu). \]
This can be represented graphically:
- Each outcome \(\mathbf{x}_n\) depends on the same latent variable \(\mu\).
- Plate notation is used to represent the repetition \(N\) times.
We can also assign a hyperprior to \(\mu\), for instance: \[ \mu \sim \text{Beta}(\alpha, \beta) \] where \(\alpha\) and \(\beta\) may be treated as deterministic parameters.
4.5.2 Conditional Independence and d-Separation
Directed graphical models can reveal conditional independence relationships directly from the graph using the concept of d-separation (Pearl, 1988).
Definition 4.13 Given disjoint node sets \(A, B, C\) in a directed acyclic graph, \(A\) is d-separated from \(B\) given \(C\), written as: \[ A \perp\!\!\!\perp B \,|\, C \] if all paths between nodes in \(A\) and \(B\) are blocked.
A path is blocked if:
- The arrows meet head-to-tail or tail-to-tail at a node in \(C\) (a path of the form \(a \rightarrow c \rightarrow b\) or \(a \leftarrow c \rightarrow b\)), or
- The arrows meet head-to-head at a node not in \(C\), and none of its descendants are in \(C\) (a path of the form \(a \rightarrow c \leftarrow b\)).
If all paths are blocked, \(A\) and \(B\) are conditionally independent given \(C\).
Example 4.9 In the graphical model:
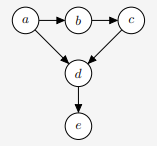
We can infer:
- \(b \perp d \,|\, a, c\)
- \(a \perp c \,|\, b\)
- \(b \not\!\perp d \,|\, c\) since \(d\) is a descendant of \(c\)
- \(a \not\!\perp c \,|\, b, e\) since \(d\) is a descendant of \(c\)
Example 4.10 d-Separation in a Bayesian Network
Consider the following directed acyclic graph (DAG):
\[ A \longrightarrow C \longrightarrow D \longleftarrow B \] We will analyze conditional independence relationships using d-separation.
We examine whether variables \(A\) and \(B\) are independent under different conditioning sets. There is exactly one undirected path between \(A\) and \(B\): \[ A \rightarrow C \rightarrow D \leftarrow B. \] This path contains a collider at node \(D\).
If we condition on nothing:
- The path contains a collider \(D\)
- Colliders block paths unless conditioned on (or their descendants are)
The path is blocked \[ A \;\perp\!\!\!\perp\; B \]
Now condition on \(C\):
- \(C\) is a chain node
- Conditioning on a chain node blocks the path
- The collider at \(D\) remains unconditioned
The path is still blocked \[ A \;\perp\!\!\!\perp\; B \mid C \]
Now condition on \(D\):
- Conditioning on a collider opens the path
The path is now unblocked \[ A \;\not\!\perp\!\!\!\perp\; B \mid D \] Knowing \(A\) gives information about \(B\) once \(D\) is known.
Suppose \(E\) is a descendant of \(D\): \[ A \rightarrow C \rightarrow D \leftarrow B, \quad D \rightarrow E \] Condition on \(E\):
- Conditioning on a descendant of a collider also opens the path
The path is unblocked \[ A \;\not\!\perp\!\!\!\perp\; B \mid E \]
Summary of Results
| Conditioning Set | Are \(A\) and \(B\) d-separated? |
|---|---|
| None | Yes |
| \(C\) | Yes |
| \(D\) | No |
| \(E\) | No |
Exercises
Exercise 4.7 Chain (No Conditioning)
\[ X \rightarrow Y \rightarrow Z \]
Question: Are \(X\) and \(Z\) independent?
- The path is a chain
- No conditioning blocks the path
Exercise 4.8 Chain (Condition on the Middle)
\[ X \rightarrow Y \rightarrow Z \]
Condition on \(Y\):
- Conditioning on a chain node blocks the path
Exercise 4.9 Fork (Common Cause)
\[ X \leftarrow Y \rightarrow Z \]
No conditioning:
- \(Y\) is a common cause
- Path is open
Exercise 4.10 Fork (Condition on the Common Cause)
\[ X \leftarrow Y \rightarrow Z \]
Condition on \(Y\):
- Conditioning on a fork node blocks the path
Exercise 4.11 Collider (No Conditioning)
\[ X \rightarrow Y \leftarrow Z \]
No conditioning:
- \(Y\) is a collider
- Colliders block paths by default
Exercise 4.12 Collider (Condition on the Collider)
\[ X \rightarrow Y \leftarrow Z \]
Condition on \(Y\):
- Conditioning on a collider opens the path