1.2 Two Ways to Read This Book
There are two main strategies for learning the mathematics that underpins machine learning. The bottom-up approach builds understanding from fundamental mathematical concepts toward more advanced ideas. This method provides a solid conceptual foundation, ensuring that each new idea rests on well-understood principles. However, for many learners, this approach can feel slow or disconnected from practical motivation, since the relevance of abstract concepts may not be immediately clear.
In contrast, the top-down approach begins with real-world problems and drills down to the mathematics required to solve them. This goal-driven strategy keeps motivation high and helps learners understand why each concept matters. The drawback, however, is that the underlying mathematical ideas can remain fragile—readers may learn to use tools effectively without fully grasping their theoretical basis.
Mathematics for Machine Learning is designed to support both approaches — foundational (Part I) and applied (Part II) — so readers can move between mathematics and machine learning freely.
This book is designed to assist readers in their understanding of the textbook Mathematics for Machine Learning. It is more of a foundational approach designed to fill in any gaps a reader might have. In particular, we aim to provide more examples in a less theoretical way. Whether you are reading from a top down or bottom up approach, this book will support your learning.
1.2.1 Part I: Mathematical Foundations
Part I develops the mathematical tools that support all major ML methods — the four pillars of machine learning:
- Regression
- Dimensionality Reduction
- Density Estimation
- Classification
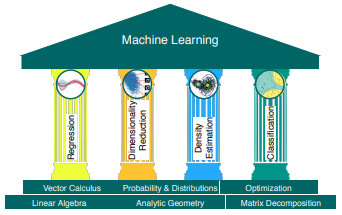
It covers:
- Linear Algebra (Ch. 2): Vectors, matrices, and their relationships.
- Analytic Geometry (Ch. 3): Similarity and distance between vectors.
- Matrix Decomposition (Ch. 4): Interpreting and simplifying data.
- Vector Calculus (Ch. 5): Gradients and differentiation.
- Probability Theory (Ch. 6): Quantifying uncertainty and noise.
- Optimization (Ch. 7): Finding parameters that maximize performance.
1.2.2 Part II: Machine Learning Applications
Part II applies the math from Part I to the four pillars:
- Ch. 8 — Foundations of ML: Data, models, and learning; designing robust experiments.
- Ch. 9 — Regression: Predicting continuous outcomes using linear and Bayesian approaches.
- Ch. 10 — Dimensionality Reduction: Compressing high-dimensional data (e.g., PCA).
- Ch. 11 — Density Estimation: Modeling data distributions (e.g., Gaussian mixtures).
- Ch. 12 — Classification: Assigning discrete labels (e.g., support vector machines).
1.2.3 Learning Path
Readers are encouraged to mix bottom-up and top-down learning:
- Build foundational skills when needed.
- Explore applications that connect math to real machine learning systems.
This modular structure makes the book suitable for both mathematical learners and practitioners aiming to deepen their theoretical understanding.