2.8 The Derivative as a Function
Differentiability
Not all functions have derivatives. While most of the functions we have dealt with have had derivatives, it is certainly not the case that they all do. Any function that has a derivative is called .
Definition: A function \(f\) is called differentiable at \(x = a\) if \(f^{\prime}(a)\) exist. A function \(f\) is called differentiable on an interval if the derivative exists for each point in that interval.
Specifically, a function can fail to be differentiable at a point \(a\) if there is a vertical tangent line, a discontinuity in the graph or if the graph has a corner.
 |
|---|
Example: Determine \(f^{\prime}(0)\) given \(g(x) = |x|\).\
Solution: We know \[\begin{align*} f^{\prime}(0) &= \lim_{h \rightarrow 0} \dfrac{f(0+h) - f(0)}{h}\\ \\ &= \lim_{h \rightarrow 0} \dfrac{|0+h| - |0|}{h}\\ \\ &= \lim_{h \rightarrow 0} \dfrac{|h|}{h}. \end{align*}\] Recall that \[|h| = \begin{cases}h & h \geq 0\\ -h & h < 0 \end{cases}.\] If we take the limit from the left, \(h < 0\). Therefore, \[\lim_{h \rightarrow 0^-} \dfrac{|h|}{h} = \lim_{h \rightarrow 0^{-}} \dfrac{-h}{h} = -1.\] If we take the limit from the right, \(h > 0\). Therefore, \[\lim_{h \rightarrow 0^+} \dfrac{|h|}{h} = \lim_{h \rightarrow 0^{+}} \dfrac{h}{h} = 1.\] Now, since the two one-sided limits are different so \(\displaystyle\lim_{h \rightarrow 0} \dfrac{|h|}{h}\) does not exist. Since the limit does not exist, neither does the derivative.
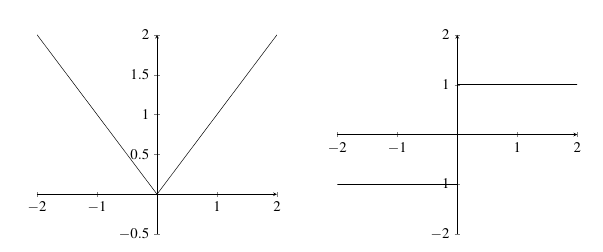 |
|---|
Practice Problems
- Determine where the following functions are differentiable.
- \(f(x) = \begin{cases} x+1 & x \geq 0 \\ x-1 & x < 0 \end{cases}\)
- \(f(x) = |x-1|\)
- \(f(x) = \begin{cases} x^2 & x \geq 0 \\ -x& x < 0 \end{cases}\)
- \(f(x) = \dfrac{1}{x^2}\)
- \(f(x) = x^{1/3}\)
- \(f(x) = \dfrac{x}{|x|}\)
- \(f(x) = \sqrt{x}\)
- \(f(x) = \sqrt{x}\)
- For each of the functions in part A, sketch a graph of the derivatives.
Differentiability & Continuity
Thus far, the functions we have been looking at have almost all been differentiable. Most functions are not differentiable. However, there is a relationship between differentiable and continuous functions.
Theorem: If \(f\) is differentiable at \(a\), then \(f\) is continuous at \(a\).
Proof: Let \(f\) be a differentiable function at a point \(x_0\). Then, we know the derivative exists. That is, \[f^{\prime}(x) = \lim_{x \rightarrow x_0} \frac{f(x) - f(x_0)}{x-x_0} = a,\] for some \(a \in \mathbb{R}\). To show that \(f\) is continuous at \(x_0\), we need to show that \[\lim_{x \rightarrow x_0} f(x) - f(x_0) = 0.\] Observe that \[\lim_{x \rightarrow x_0} f(x) - f(x_0) = \lim_{x \rightarrow x_0} \left[ \frac{f(x) - f(x_0)}{x-x_0} \right] \cdot \lim_{x \rightarrow x_0} (x-x_0) = a \cdot \lim_{x \rightarrow x_0} (x-x_0) = 0.\] Therefore, since \(\displaystyle\lim_{x \rightarrow x_0} f(x) - f(x_0) = 0\), we know the function is continuous.
We know that \(f(x) = |x|\) is a continuous function on \(\mathbb{R}\). So, we know that the converse of the theorem does not hold since we have seen that \(y = |x|\) is not differentiable at 0. Another example worth noting is \(y = \sqrt[3]{x}\). This function is continuous on \(\mathbb{R}\) but is not differentiable at 0 since it has a vertical tangent line. The function \(y = x^{2/3}\) is again continuous but not differentiable at \(0\) since it has a cusp. Remember, not all continuous functions are differentiable - though many are.
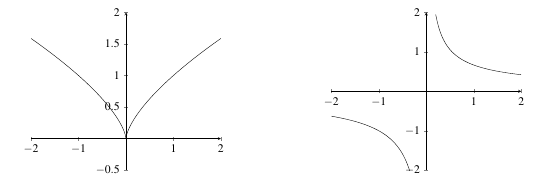 |
|---|
Practice Problems
- Show that the function is continuous but not differentiable at the indicated point:
- \(f(x) = \sqrt[3]{x}\) at \(x = 0\)
- \(f(x) = \sqrt[3]{(x-2)^2}\) at \(x = 2\)
- \(f(x) = \begin{cases} x^2 + 1 & x \leq 1 \\ 2x & x >1 \end{cases}\)
Suppose that a function \(f\) is differentiable at \(x_0\). Define \(g(x) = f(mx+b)\) where \(m\) and \(b\) are constants. Show that if \(x_1\) is any point at which \(mx_1+b = x_0\), then \(g\) is differentiable and \(g^{\prime}(x_1) = mf^{\prime}(x_0)\).\
Draw a graph with the following characteristics:
- Exists on \([-5,5]\)
- Differentiable on \([-5,-3)\)
- Not continuous at -3
- Differentiable on \([-3,2]\)
- Continuous at 2
- Not differentiable at 2
- Differentiable on \((2,5]\)
Find constants \(a\) and \(b\) so that the following function is continuous and differentiable everywhere \[f(x) = \begin{cases} ax + b & x \leq 1 \\ 2x^2 & x \geq 1 \end{cases}.\]
Where is the following function differentiable \[f(x) = |x-2| + |x+1|.\]
Explain why \[f(x) = \begin{cases} x^2 - 1 & x \leq 1 \\ x^2 + 1 & x \geq 1 \end{cases}\] is not differentiable at \(x = 1\) even though the derivative of \(x^2-1\) and \(x^2 + 1\) are the same.
Notation
In differential and integral calculus, there is no single uniform notation for differentiation. Over the years, several different notations have emerged. Each notation typically is contextually advantageous in some area. However, no one notation has the benefit of being the most advantageous in all cases.
The notation that we have used so far is attributed to Lagrange. In Lagrange notation, a prime mark denotes the derivative. For example, \(f^{\prime}(x)\). If we wanted to take the derivative of the derivative (ie, a second derivative), we use a second prime mark, \(f^{\prime \prime}(x)\). When we are taking a derivative higher than four, most authors switch to Arabic numerals in brackets. For example \(f^{(6)}(x)\) for a \(6^{th}\) derivative. If \(y = f(x)\), many authors will write \(y^{\prime}\) to indicate the derivative of \(y\) as a short hand for \(f^{\prime}(x)\).
| \(\;\) | Notation |
|---|---|
| Function | \(f(x), \;\; y\) |
| Derivative | \(f^{\prime}(x), \;\; y^{\prime}\) |
| \(2^{nd}\) Derivative | \(f^{\prime \prime }(x), \;\; y^{\prime \prime}\) |
| Higher Derivative | \(f^{(n)}(x), \;\; y^{(n)}\) |
Example: From one of the previous problems, if \(f(x) = x^3 + x - 5\), we have \(f^{\prime}(x) = 3x^2 + 1\). We can also write: \(y = x^3 + x - 5 \Longrightarrow y^{\prime}(x) = 3x^2 + 1\).
Leibnitz notation is slightly different. If \(y = f(x)\), we denote the first derivative of \(f\) by \(\frac{dy}{dx}\). So here, \(f^{\prime}(x) = \frac{dy}{dx}\). Another way to interpret Leibnitz notation is by writing \(\frac{d}{dx} f(x) = \frac{dy}{dx}\). The notation \(\frac{d}{dx} f(x)\) can be interpreted as ``we are about to take the derivative of \(f(x)\)’’. For higher derivatives, we can write \(\frac{d^2y}{dx^2}\) in place of \(f^{\prime \prime}\).
| \(\;\) | Lagrange Notation | Leibnitz Notation |
|---|---|---|
| Function | \(f(x), \;\; y\) | \(f(x), \;\; y\) |
| Derivative | \(f^{\prime}(x), \;\; y^{\prime}\) | \(\frac{df}{dx}, \;\; \frac{dy}{dx}\) |
| \(2^{nd}\) Derivative | \(f^{\prime\prime }(x), \;\; y^{\prime \prime}\) | \(\frac{d^2f}{dx^2}, \;\; \frac{d^2y}{dx^2}\) |
| Higher Derivative | \(f^{(n)}(x), \;\; y^{(n)}\) | \(\frac{d^nf}{dx^n}, \;\; \frac{d^ny}{dx^n}\) |
Example: From one of the previous problems, if \(f(x) = x^3 + x - 5\), we have \(f^{\prime}(x) = 3x^2 + 1\). We can also write: \[\begin{align*} f(x) &= x^3 + x - 5 \Longrightarrow \frac{df}{dx} = 3x^2 + 1\\ \\ f(x) &= x^3 + x - 5 \Longrightarrow \frac{d}{dx}f(x) = 3x^2 + 1\\ \\ y &= x^3 + x - 5 \Longrightarrow \frac{dy}{dx} = 3x^2 + 1\\ \\ &\frac{d}{dx}\left[x^3 + x - 5\right] = 3x^2 + 1 \end{align*}\]
One final notation is Euler’s notation. Here we use \(Df\) to mean \(f^{\prime}(x)\). Higher derivatives are written \(D^2f\) for \(f^{\prime \prime}(x)\), etc.
Example: Given a function \(y = f(x)\), all of the following are equivalent and represent the derivative of \(f(x)\) with respect to x. \[f^{\prime}(x) = y^{\prime} = \dfrac{d f}{dx} = \dfrac{dy}{dx} = \dfrac{d}{dx}f(x) = \dfrac{d}{dx} y.\] If we want to evaluate the derivative at a point \(x = a\), all of the following are equivalent notations: \[f^{\prime}(a) = y^{\prime} \bigg\rvert_{x=a} = \dfrac{df}{dx} \bigg\rvert_{x = a} = \dfrac{dy}{dx} \bigg\rvert_{x = a}.\]
The context in which each of these notations is advantageous will be unclear for a while. For now, we will use each one interchangeably.